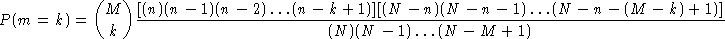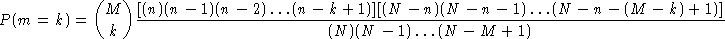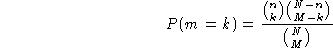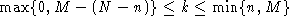Hypergeometric Distribution
Computations
Follow the links to compute the probability distribution, cumulative
distribution function or quantiles of the hypergeometric distribution.
Table of
the Probability Distribution
Table of the Cumulative Distribution
Function
Information
The hypergeometric distribution is arises as a model for sampling
without replacement from a population consisting of two types
of items.
To be specific, think of selecting M people at random from a
group of N people, n of whom are female. Let m
represent the number of females chosen. Then m has a hypergeometric
distribution given by
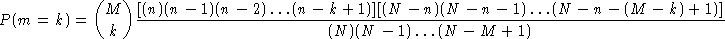
A more compact way of writing this formula is
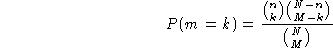
In either case, the formula's validity is restricted to the set of possible
values for m, namely, it is valid for
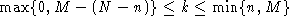
-
The mean of the hypegeometric distribution is M(n/N).
-
The variance of the hypergeometric distribution is
M(n/N)[1-(n/N)][(N-M)/(N-1)].
Back to the
Probability Distribution page.