Fabrice BAUDOIN, Department of Mathematics, Purdue
University,
Generalized Bochner formulas and subelliptic heat kernels estimates.
We will prove
generalized Bochner formulas for some subelliptic Hormander's type operators.
As a consequence, we shall derive Li-Yau type estimates for the corresponding
semigroup and heat kernels Gaussian
bounds.
Alexandra CHRONOPOULOU, Department of Statistics, Purdue
University,
Variations and Hurst Index Estimation for non-Gaussian Hermite
processes.
Using
multiple stochastic integrals and the Malliavin calculus, we analyze the
asymptotic behavior of quadratic variations for a class of non-Gaussian
self-similar processes, the Hermite processes (
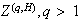). The process
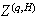has stationary, H-self-similar increments that exhibit long-memory, identical
to that of the fractional Brownian motion (fBm). For
,
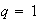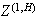is fBm, which is Gaussian; for
,
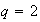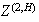is the Rosenblatt process, which lives in the second Wiener chaos; for any
,
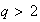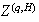is a process in the qth Wiener chaos. We prove a reproduction property for
this class of processes in the sense that the terms appearing in the chaotic
decomposition of their variations give rise to other Hermite processes of
different orders and with different Hurst parameters. We also study the
behavior of the variations of the Roseblatt process using longer filters. We
apply our results to construct a strongly consistent estimator for the
self-similarity parameter H from discrete observations of the process. The
asymptotic distribution of the estimator depends explicitly on the order and
the length of the filter. We compare the numerical values of the asymptotic
variances for various choices of filters, including finite-difference and
wavelet-based filters. This is joint work with Ciprian Tudor (Sorbonne I) and
Frederi Viens (Purdue
University).
José E. FIGUEROA-LOPEZ, Department of Statistics, Purdue
University,
Optimal
portfolios and admissible strategies in a Lévy market.
In this talk, we give
characterizations for the dual solution of Merton's portfolio optimization
problem in a non-Markovian market driven by a Lévy process. Our approach
is based on a multiplicative optional decomposition for nonnegative
supermartingales due to F\"ollmer and Kramkov as well as a closure property
for integrals with respect to a fixed Poisson random measure. Under certain
constraints on the jumps of the price process, we characterize explicitly the
admissible trading strategies and show that the dual solution is a
risk-neutral local
martingale.
Ionuţ FLORESCU, Department of Mathematical Sciences,
Stevens Institute of
Technology,
A study
of an integro-differential parabolic problem arising in Mathematics of
Finance.
In Finance
one of the most studied problems is pricing options when the underlying equity
follows a stochastic process. If the underlying process is a regular diffusion
the problem is reduced to solving a Partial Differential Equation. However, if
the underlying process possesses jumps (or more general a Lévy component)
an integral term arises in the defining equation due to the associated Levy
measure. This produces the so called Partial Integro-Differential Equations.
Problems of existence, uniqueness and determination of solutions for such
equations are still open. In this talk I will present a proof of existence on
general domains under suitable conditions on the integral operator. The proof
is based on the method of upper and lower solutions and also provides an
algorithm to approximate the solution. The work is based on the collaboration
with Prof. Maria C. Mariani from University of Texas at El
Paso.
Carlo MARINELLI, Institute for Applied Mathematics,
Universität Bonn,
Germany,
Ergodicity
for nonlinear stochastic evolution equations with multiplicative Poisson
noise.
We study the
asymptotic behavior of solutions to stochastic evolution equations with
monotone drift and multiplicative Poisson noise in the variational setting,
thus covering a large class of (fully) nonlinear partial differential
equations perturbed by jump noise. In particular, we provide sufficient
conditions for the existence, ergodicity, and uniqueness of invariant
measures. Furthermore, under mild additional assumptions, we prove that the
Kolmogorov equation associated to the stochastic equation with additive noise
is solvable in
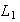spaces with respect to an invariant
measure.
Ivan NOURDIN, Laboratoire de Probabilités,
Université Paris 6,
France,
Universal
Gaussian fluctuations of non-Hermitian matrix ensembles.
I will explain how to
prove multi-dimensional central limit theorems for the spectral moments (of
arbitrary degrees) associated with random matrices with real-valued i.i.d.
entries, satisfying some appropriate moment conditions. The used techniques
rely on a universality principle for the Gaussian Wiener chaos as well as some
combinatorial estimates. Unlike other related results in the probabilistic
literature, the fact that the law of the entries has a density with respect to
the Lebesgue measure is not required. This talk is based on a joint work with
Giovanni Peccati (Paris Ouest), and use an invariance principle obtained in a
joint work with G. P. and Gesine Reinert
(Oxford).
David NUALART, Department of Mathematics, University of
Kansas,
Central
limit theorem for the modulus of continuity of the Brownian local
time.
In this talk
we present a proof of the central limit theorem for the modulus of continuity
of the Brownian local time based on the Clark-Ocone stochastic integral
representation formula and an asymptotic version of Knight's theorem. We plan
also to discuss the application of the techniques of Malliavin calculus to
derive central limit theorems for Skorohod stochastic
integrals.
Giovanni PECCATI, Centre de Recherche MODAL'X,
Université Paris Ouest
Nanterre,
and
Laboratoire de Statistique Théorique et Appliquée, Université
Paris 6, France,
Stein's method meets Malliavin calculus: from Berry-Esseen to
universality.
We
discuss some applications of Malliavin calculus and Stein's method to the
derivation of explicit bounds in limit theorems involving functionals of a
general Gaussian field. Some applications to isotropic spherical fields are
described. A universality result is also presented: this is a crucial tool in
the CLT for spectral measures of non-Hermitian random matrix ensembles
discussed in Nourdin's talk. Based on joint works with I. Nourdin (Paris 6)
and G. Reinert (Oxford).
Michael RÖCKNER, Fakultät für Mathematik,
Universität Bielefeld,
Germany,
Fokker--Planck equations on Hilbert spaces.
We consider a
stochastic differential equation in Hilbert space with time dependent
coefficients for which no general existence and uniqueness results are known.
We prove, under suitable assumptions, existence and uniqueness of a measure
valued solution, for the corresponding Fokker-Planck equation. In particular,
we verify the Chapman-Kolmogorov equations and get an evolution system of
transition probabilities for the stochastic dynamics informally given by the
stochastic differential
equation.
Francesco RUSSO, Institut Galilée, Mathématiques,
Université Paris 13,
and Projet MATHFI, INRIA Rocquencourt & Cermics Ecole des
Ponts, France,
Probabilistic representation of a partial differential equation with
monotone discontinuous coefficients and related fields.
We consider a partial
differential equation over the the real line with monotone discontinuous
coefficients and prove a probabilistic representation of its solution in terms
of an associated microscopic diffusion. We will distinguish between two
different situations: the so-called non-degenerate and
degenerate cases. In the first case we show existence and
uniqueness, however in the second one for which we only show existence. Some
comments about an associated stochastic PDE with multiplicative noise will be
provided. This talk is based on two joint papers: the first with Ph. Blanchard
and M. Röckner, the second one with V. Barbu and M.
Röckner.
Jason SWANSON, Department of Mathematics, University of
Central Florida,
Fluctuations of the empirical quantiles of independent Brownian
motions.
We
consider
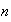independent, identically distributed one-dimensional Brownian motions,
,
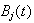where
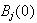has a rapidly decreasing, smooth density function
.
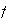The empirical quantiles, or pointwise order statistics, are denoted by
,
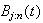and we are interested in a sequence of quantiles
,
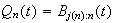where
.
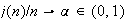This sequence converges in probability in
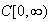to
,
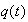the
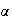-quantile
of the law of
.
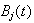Our main result establishes the convergence in law in
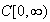of the fluctuation processes
.
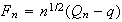The limit process
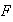is a centered Gaussian process and we derive an explicit formula for its
covariance function. We also show that
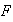has many of the same local properties as
,
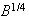the fractional Brownian motion with Hurst parameter
.
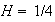For example, it is a quartic variation process, it has Hölder continuous
paths with any exponent
,
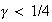and (at least locally) it has increments whose correlation is negative and of
the same order of magnitude as those of
.
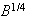